Gambler's Ruin and Sequential Testing
Random Walks
Suppose we start with n dollars, and make a sequence of bets. For each bet, we win 1 dollar with probability p, and lose 1 dollar with probability 1 − p. We quit if either we go broke, in which case we lose, or when we reach T = n + m dollars, that is, when we win m dollars. For example, in Roulette, p = 18/38 = 9/19 ∼ 0.473. If n = 100 dollars, and m = 100 dollars, then T = 200 dollars. What are the odds we win 100 dollars before losing 100 dollars? Most folks would think that since 0.473 ∼ 0.5, the odds are not so bad. In fact, as we will see, we win before we lose with probability at most 1/37649!
Boundary Crossing
This random walk is a special type of random walk where moves are independent of the past. If p = 1/2, the random walk is unbiased and is called a .For p ≠ 1/2, the random walk is biased (). If the walk hits a boundary (0 or n + m), then we stop playing.
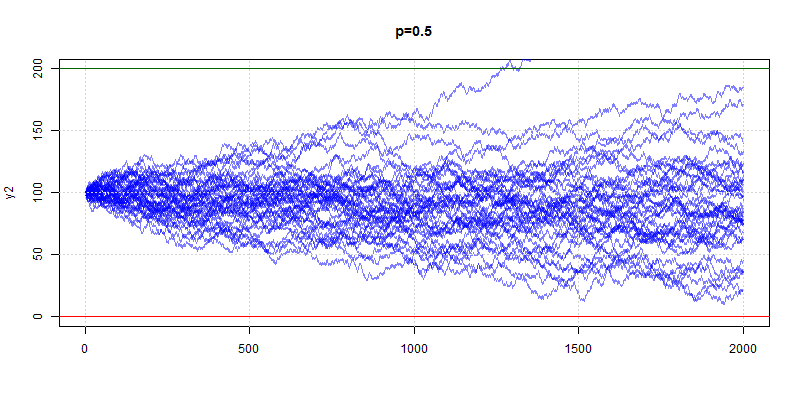
Unfair coin flipping
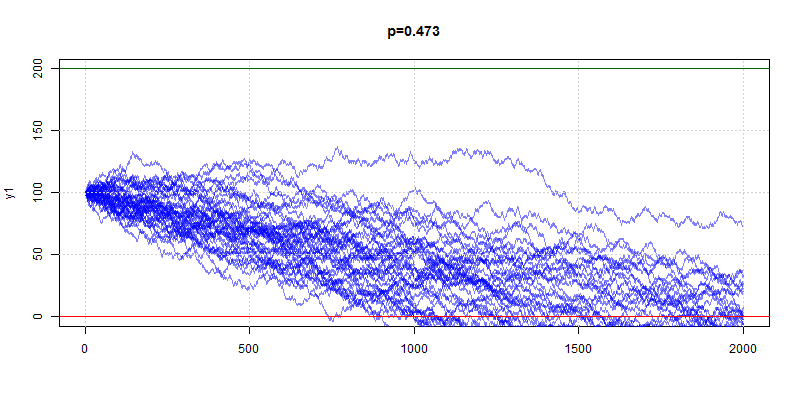
Try for yourself
Probability to win
Let’s figure out the probability that we gain m before losing n. To set things up formally, let W be the event we hit T before we hit 0, where T = n + m. Let Dt be a random variable that denotes the number of dollars we have at time step t. Let Pn = ℙ(W|D0 = n) be the probability we get T before we go broke, given that we start with n dollars. Our question then, is what is Pn ? We’re going to use a recursive approach. Pn = p ⋅ Pn + 1 + (1 − p) ⋅ Pn − 1, for 0 < n < T
Solving it for p < 0.5 yields
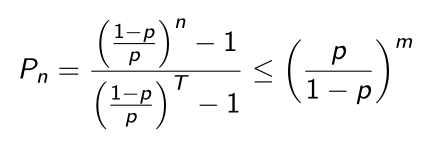
This last expression is even independent of n, and exponentially small in m.
Probability to win
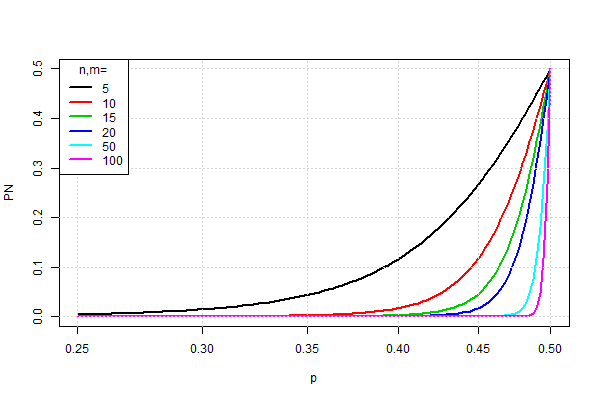
Intuition off ?
Why does this seem to run against our intuition ? Normally we would think that the probability of winning 100 dollars before losing 200 dollars is better than winning 10 before losing 10, i.e., that the ratio is what matters. In fact, the ratio is what matters if the game is fair, i.e., if p = 1/2. In that case, we simply have Pn = n/(n + m) = n/T In this case, if n = 200 and m = 100, we have Pr(Win)=200/300=2/3. On the other hand, if n = 10 and m = 10, then Pr(Win)=10/20=1/2. Thus, actually, now we are more likely to win in the first case!
So the trouble is that our intuition tells us that if the game is almost fair, then we expect the results to be almost the same as if the game were fair. It turns out this is not the case!